Trong toán học và khoa học máy tính, việc tìm kiếm nghiệm của một phương trình hoặc hệ phương trình đóng vai trò quan trọng trong nhiều lĩnh vực, từ giải quyết bài toán tối ưu đến mô hình hóa các hiện tượng tự nhiên. “So Sánh Nghiệm” là một phương pháp quan trọng được sử dụng để phân tích và đánh giá các nghiệm tìm được, từ đó đưa ra kết luận chính xác và hiệu quả hơn.
Bài viết này sẽ đi sâu vào tìm hiểu về phương pháp so sánh nghiệm, bao gồm các kỹ thuật phổ biến, ưu nhược điểm và ứng dụng thực tiễn của nó.
Các Phương pháp So sánh Nghiệm Phổ biến
Tùy thuộc vào tính chất của bài toán và loại nghiệm cần so sánh, chúng ta có thể sử dụng nhiều phương pháp khác nhau. Dưới đây là một số phương pháp phổ biến:
1. So sánh Trực tiếp
Đây là phương pháp đơn giản nhất, được sử dụng khi ta có thể tính toán trực tiếp giá trị của các nghiệm. Bằng cách so sánh trực tiếp các giá trị này, ta có thể xác định nghiệm nào lớn hơn, nhỏ hơn hoặc bằng nhau.
Ví dụ: So sánh nghiệm của hai phương trình:
- x + 2 = 5 => x = 3
- 2x – 1 = 5 => x = 3
Trong trường hợp này, ta thấy hai phương trình có cùng một nghiệm x = 3.
 So sánh nghiệm trực tiếp
So sánh nghiệm trực tiếp
2. So sánh Sai số
Phương pháp này thường được sử dụng khi ta không thể tính toán chính xác nghiệm của phương trình. Thay vào đó, ta sẽ tìm kiếm nghiệm gần đúng và so sánh sai số của chúng. Sai số càng nhỏ, nghiệm càng chính xác.
Ví dụ: Sử dụng phương pháp Newton-Raphson để tìm nghiệm gần đúng của phương trình x^2 – 2 = 0.
Giả sử ta tìm được hai nghiệm gần đúng là x1 = 1.414 và x2 = 1.4142. Sai số của hai nghiệm này lần lượt là |x1^2 – 2| và |x2^2 – 2|. Bằng cách so sánh hai sai số này, ta có thể xác định nghiệm nào chính xác hơn.
3. So sánh Đồ thị
Đối với các phương trình có thể biểu diễn dưới dạng đồ thị, ta có thể so sánh nghiệm bằng cách vẽ đồ thị của chúng trên cùng một hệ trục tọa độ. Giao điểm của các đồ thị sẽ là nghiệm chung của các phương trình.
Ví dụ: So sánh nghiệm của hai phương trình y = x + 1 và y = -x + 3.
Bằng cách vẽ đồ thị của hai phương trình này, ta thấy chúng cắt nhau tại điểm (1, 2). Do đó, nghiệm của hệ phương trình là x = 1, y = 2.
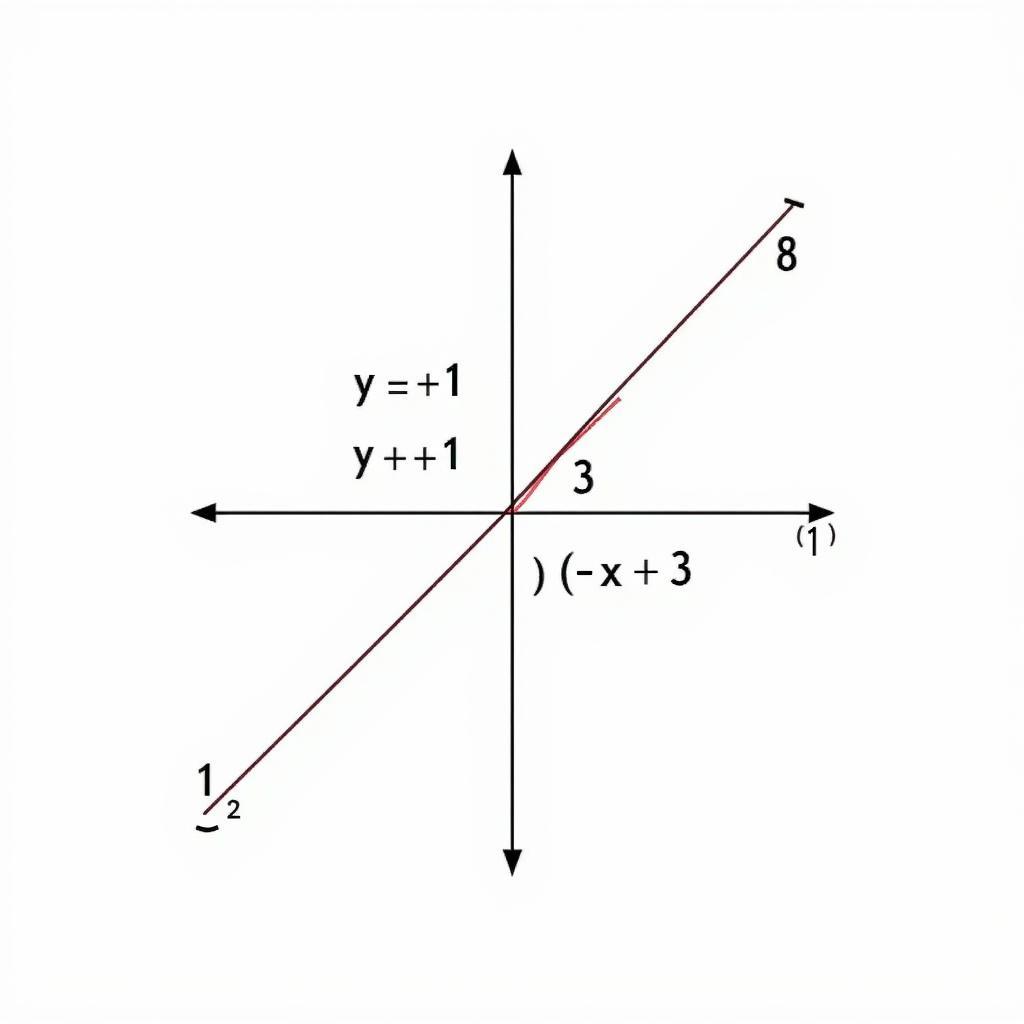 So sánh nghiệm bằng đồ thị
So sánh nghiệm bằng đồ thị
Ưu nhược điểm của phương pháp so sánh nghiệm
Ưu điểm:
- Dễ hiểu và dễ thực hiện: Hầu hết các phương pháp so sánh nghiệm đều khá trực quan và dễ thực hiện, ngay cả khi không có kiến thức toán học chuyên sâu.
- Hiệu quả trong nhiều trường hợp: So sánh nghiệm là một phương pháp linh hoạt, có thể áp dụng cho nhiều loại phương trình và hệ phương trình khác nhau.
- Hỗ trợ ra quyết định: Bằng cách so sánh các nghiệm, ta có thể đánh giá hiệu quả của các phương pháp giải bài toán khác nhau và lựa chọn phương pháp tối ưu nhất.
Nhược điểm:
- Khó khăn khi so sánh nghiệm phức tạp: Đối với các phương trình có nghiệm phức tạp, việc so sánh nghiệm có thể trở nên khó khăn và mất thời gian.
- Phụ thuộc vào độ chính xác của phép tính: Sai số trong quá trình tính toán có thể ảnh hưởng đến kết quả so sánh nghiệm.
- Không phải lúc nào cũng cung cấp đầy đủ thông tin: Trong một số trường hợp, việc so sánh nghiệm chỉ cung cấp thông tin về giá trị của nghiệm mà không cho biết gì về tính chất hoặc ý nghĩa của chúng.
Ứng dụng của so sánh nghiệm trong thực tiễn
So sánh nghiệm có nhiều ứng dụng quan trọng trong thực tế, bao gồm:
- Tối ưu hóa: Tìm kiếm giá trị tối ưu của một hàm số, ví dụ như tìm kiếm kích thước tối ưu của một sản phẩm để giảm thiểu chi phí sản xuất.
- Mô hình hóa: Xây dựng các mô hình toán học để mô tả các hiện tượng tự nhiên, ví dụ như mô hình dự đoán thời tiết hoặc mô hình lan truyền dịch bệnh.
- Phân tích dữ liệu: So sánh các mô hình thống kê khác nhau để tìm ra mô hình phù hợp nhất với dữ liệu.
- Khoa học máy tính: Phát triển các thuật toán tìm kiếm và sắp xếp dữ liệu hiệu quả.
Kết luận
So sánh nghiệm là một phương pháp quan trọng trong toán học và khoa học máy tính, giúp chúng ta phân tích và đánh giá các nghiệm của phương trình và hệ phương trình. Bằng cách hiểu rõ các phương pháp so sánh nghiệm khác nhau, ưu nhược điểm và ứng dụng của chúng, ta có thể áp dụng hiệu quả phương pháp này vào giải quyết các bài toán thực tế.
Bạn cần hỗ trợ?
Liên hệ ngay với chúng tôi để được tư vấn và hỗ trợ tốt nhất!
- Số điện thoại: 0372991234
- Email: [email protected]
- Địa chỉ: 212 Hàm Nghi, Hà Nội
Chúng tôi có đội ngũ chuyên viên giàu kinh nghiệm, sẵn sàng hỗ trợ bạn 24/7!
