Bài toán kiểm tra tính chia hết là một dạng bài tập phổ biến trong chương trình toán học lớp 6. Trong đó, việc xác định xem biểu thức “2n + 9” có chia hết cho “n + 3” hay không đòi hỏi vận dụng linh hoạt các kiến thức về phép chia, ước số, bội số. Bài viết này sẽ giúp bạn hiểu rõ cách giải quyết bài toán này một cách chi tiết và cung cấp các bài tập vận dụng để củng cố kiến thức.
Phương Pháp Giải Toán Chia Hết Cho Biểu Thức
Để giải quyết bài toán xác định tính chia hết của biểu thức “2n + 9” cho “n + 3”, chúng ta có thể áp dụng các phương pháp sau:
1. Biến đổi biểu thức:
- Ta có thể biến đổi biểu thức “2n + 9” thành dạng “2(n + 3) + 3”.
- Như vậy, để “2n + 9” chia hết cho “n + 3” thì 3 phải chia hết cho “n + 3”.
2. Tìm ước số:
- Ta cần tìm các ước số của 3, bao gồm: -3, -1, 1, 3.
- Từ đó, ta giải các phương trình: n + 3 = -3, n + 3 = -1, n + 3 = 1, n + 3 = 3 để tìm ra giá trị của n.
3. Kiểm tra kết quả:
- Sau khi tìm được các giá trị của n, ta thay ngược lại vào biểu thức ban đầu “2n + 9” để kiểm tra xem kết quả có chia hết cho “n + 3” hay không.
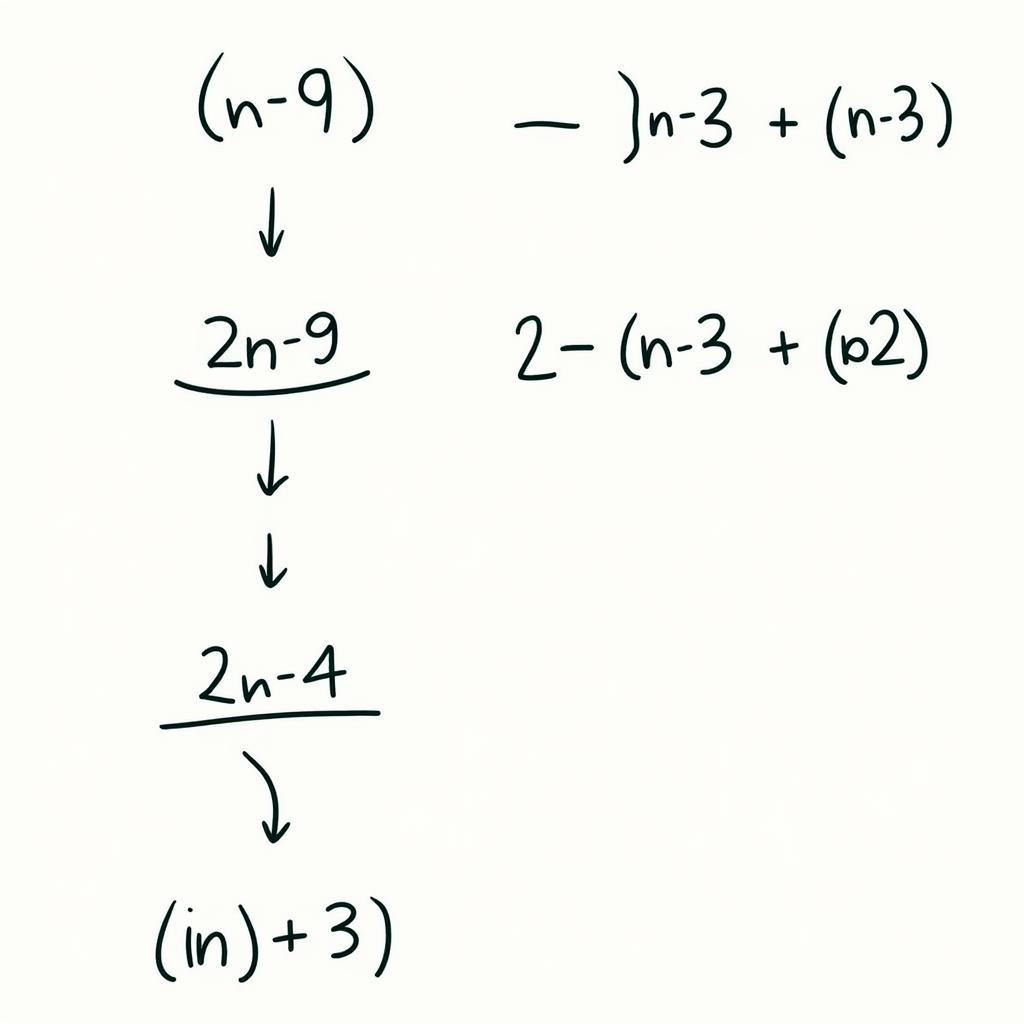 Biểu diễn biến đổi biểu thức 2n+9
Biểu diễn biến đổi biểu thức 2n+9
Bài Tập Vận Dụng
Để giúp bạn nắm vững kiến thức về tính chia hết của biểu thức “2n + 9” cho “n + 3”, hãy cùng thực hành với một số bài tập vận dụng sau:
Bài tập 1: Tìm các giá trị nguyên của n để “2n + 9” chia hết cho “n + 3”.
Bài tập 2: Chứng minh rằng với mọi số nguyên n, biểu thức “(2n + 9)(n + 3)” luôn chia hết cho “n + 3”.
Bài tập 3: Tìm giá trị nhỏ nhất của biểu thức “|(2n + 9) – 3(n + 3)|” với n là số nguyên.
 Hình ảnh minh họa bài tập vận dụng về tính chia hết của biểu thức
Hình ảnh minh họa bài tập vận dụng về tính chia hết của biểu thức
Kết Luận
Việc xác định tính chia hết của biểu thức “2n + 9” cho “n + 3” đòi hỏi sự kết hợp linh hoạt giữa các kiến thức về phép chia, ước số, bội số. Bằng cách biến đổi biểu thức, tìm ước số và kiểm tra kết quả, ta có thể dễ dàng giải quyết bài toán này. Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức bổ ích và giúp bạn tự tin hơn trong việc giải quyết các bài toán liên quan đến tính chia hết.
FAQ
-
Làm thế nào để biến đổi biểu thức “2n + 9” thành dạng “2(n + 3) + 3”?
- Ta có thể viết lại “2n + 9” thành “2n + 6 + 3”.
- Sau đó, nhóm hai số hạng đầu tiên lại và đặt 2 làm nhân tử chung, ta được “2(n + 3) + 3”.
-
Tại sao phải biến đổi biểu thức “2n + 9” thành dạng “2(n + 3) + 3”?
- Việc biến đổi này giúp ta dễ dàng nhận thấy rằng để “2n + 9” chia hết cho “n + 3” thì 3 phải chia hết cho “n + 3”.
-
Ngoài cách tìm ước số, còn cách nào khác để giải bài toán này không?
- Ta có thể sử dụng phép chia đa thức để kiểm tra tính chia hết, tuy nhiên cách này thường phức tạp hơn đối với học sinh lớp 6.
 Hình ảnh minh họa giải thích các câu hỏi thường gặp
Hình ảnh minh họa giải thích các câu hỏi thường gặp
Bạn Cần Hỗ Trợ?
Nếu bạn cần hỗ trợ thêm về bài toán chia hết hoặc các vấn đề liên quan đến toán học, hãy liên hệ với chúng tôi:
Số Điện Thoại: 0372991234
Email: [email protected]
Hoặc đến địa chỉ: 212 Hàm Nghi, Hà Nội.
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
